北京师范大学系统科学学院-yb亚博全站首页

的性质可以直接通过动力学方程来研究，但是对许多真实的复杂系统，其动力学方程是未知的，从不完整或噪声数据中发掘系统的是一大挑战。尽管传统方法如延迟坐标嵌入法和koopman算子理论都部分解决了这个问题，但它们常常在数据需求或系统渐近行为的准确性方面还存在局限。现有的机器学习方法虽然在预测瞬态行为上有成效，但往往无法准确捕捉系统的长时行为特别是驱动系统演化背后的。

近期，machine learning: science and technology 期刊发表了题为“data-driven dynamics reconstruction using rbf network”的论文，使用（rbf）网络隐式地近似复杂系统动力学方程，准确再现了lorenz、chen系统和心脏动力学系统的轨迹、定态点和局部分岔，并成功区分健康人和心脏病患者。该论文的第一作者是系统科学学院的硕士生杜淙淙，通讯作者是教授，论文于2023 年 10 月 26 日正式发表并被期刊官方网站收入合辑: focus on generative ai in science。

论文旨在用径向基函数（rbf）网络近似复杂动力学系统的演化方程。该方法有效且高效，成功应用于经典的混沌系统和心脏动力学系统，展示了其在实际系统中的应用潜力和揭示动力学性质的能力，为理论研究和实际应用提供了新的视角和工具。

该方法包括三个步骤，首先从观测数据的数值微分以获得相应的导数序列，然后通过有监督的学习训练一个径向基函数(rbf)网络，最后把训练完成的网络看作是系统演化的动力学方程开展常规的动力学分析。这个分析可以近似地反映原系统的动力学性质。

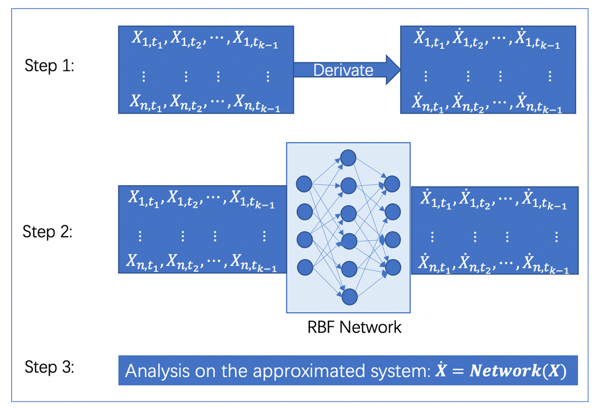
图1 使用rbf网络对动力学系统进行重构的三个关键步骤

研究中成功地利用rbf网络重构了经典的lorenz和chen系统。通过粒子群(pso)算法寻找了系统的平衡点，并在此基础上绘制出了系统的分支图，如图2（c）所示。这些重构结果与理论值高度一致。

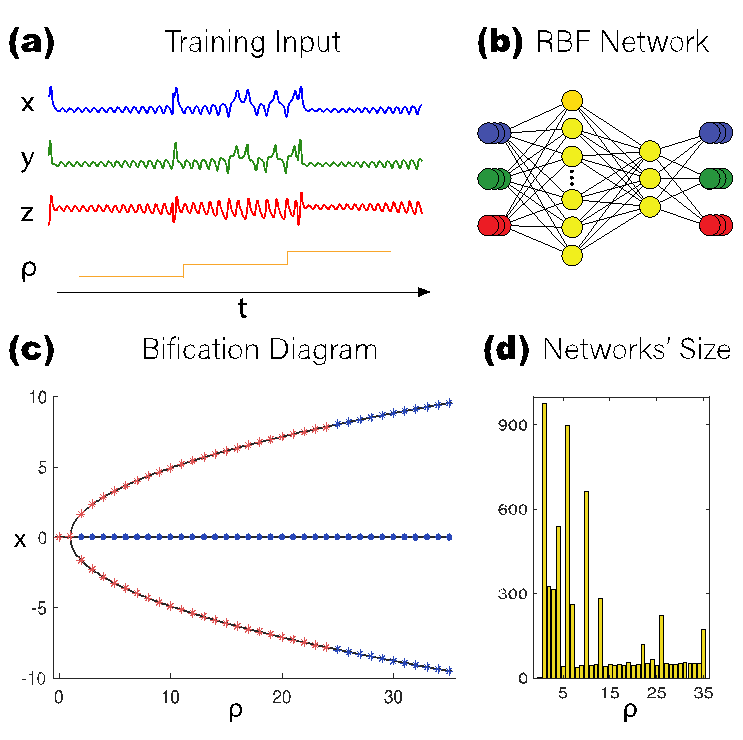
图2 lorenz系统的重建过程及结果

更重要的是，这一方法也被成功应用于心电图（ecg）数据。对249名被试的心电数据，依据其疾病状态进行分组训练。通过pso算法找到了各自网络的平衡点。如图3所示，健康与患病个体在平衡点上呈现出明显的分簇，证实了rbf网络不仅可以重构心脏动力学系统，还能捕获到原始系统的关键动力学特征。

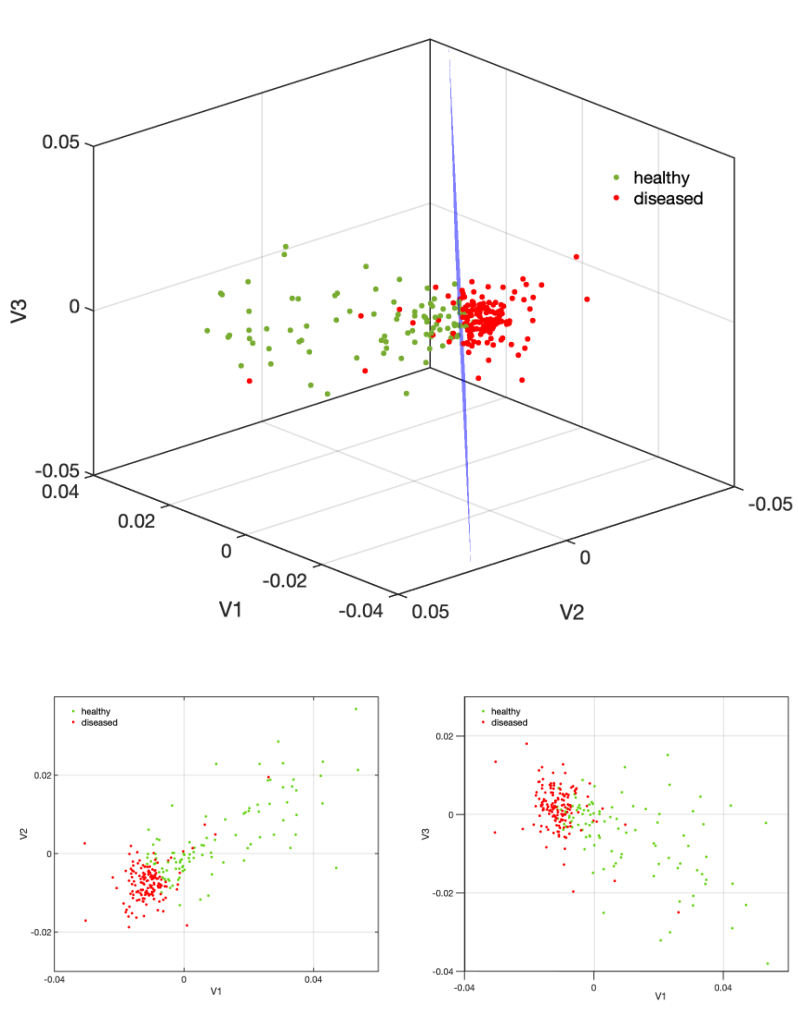
图3 心脏系统重建结果

总体而言，本研究提出了一种数据驱动的方法，通过使用rbf网络来近似复杂动力学系统的演化方程。该方法在经典混沌系统和实际应用（如心脏动力学）中都表现出色，为解决基于观测数据构建动力学方程的难题提供了一种思路，为理论研究和医疗诊断提出一条可能的新路径。

该工作得到国家自然科学基金(no.32171094)和国家重点研发计划(2019yfa0709503)的支持。

文章信息：du, c., wang, x., wang, z., & wang, d. (2023). data-driven dynamics reconstruction using rbf network. machine learning: science and technology, 4(4), 045016. doi:10.1088/2632-2153/acec31

文章链接：

供稿：王大辉

编辑：郝林青

审核：王大辉