北京师范大学系统科学学院-yb亚博全站首页

自组织临界现象是指大量个体组成的系统因外部能量输入和个体间相互作用而自发达到临界状态的神奇现象。当系统处于自组织临界状态时，微小的局部变化可被不断放大、扩延至整个系统。1987年，bak、汤超和wiesenfeld引入被称为btw模型的沙堆模型来说明自组织临界现象的形成和特点，建立了自组织临界性（soc）的概念。在这个模型中，系统会自发的演化到临界状态，展现雪崩行为，雪崩大小的分布服从幂律行为。后续人们发现，自然界中很多现象都表现出类似的规律，被认为是自然界中的自组织临界行为，比如地震和降雨等。

当前，自组织临界行为的研究面临着两大挑战：一方面需要处理非平衡系统，另外还需寻找合适的序参量来描述其相变和临界行为。陈晓松教授团队近年来发展的本征微观方法能统一处理平衡态和非平衡态系统，通过本征微观态的凝聚能够精准确定相变涌现的相及其序参量。此方法已成功应用于各种经典与量子的平衡态与非平衡态系统。最近，本征微观态方法被应用于研究沙堆模型的自组织临界现象，发现吸收态到自组织临界态的相变对应着本征微观态的凝聚，通过研究本征微观态的标度和临界行为可确定自组织临界现象的临界指数。

沙堆模型从吸收态到临界态的相变过程中，系统本征微观态的概率随之增加，类似于平衡系统（如伊辛模型）中观察到的相变现象，进一步证实本征微观态方法具有统一描述平衡态和非平衡态系统相变的能力。并且，第二和第三本征微观态的概率展现了临界相变前的早期预警信号（见图1）。

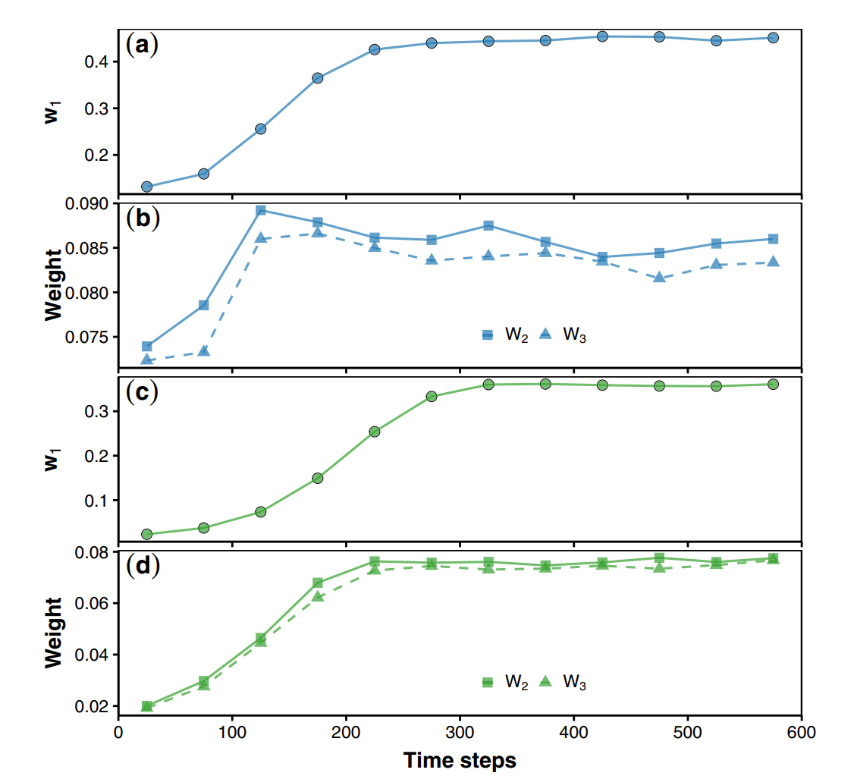
图1. 吸收态向自组织临界态的演化与本征微观态的凝聚。（a）和（b）展示btw模型的结果，随机规则的manna模型的结果展示在（c）和（d）。

图2展示的本征微观态的空间分布显示了雪崩发生的特征尺度，它随系统尺度成比例地发生变化。采用系统尺度对空间坐标进行约化后，本征微观态的空间分布具有不变性（见图2）。研究工作还进一步提出了本征微观态时间演化对应的标度关系。

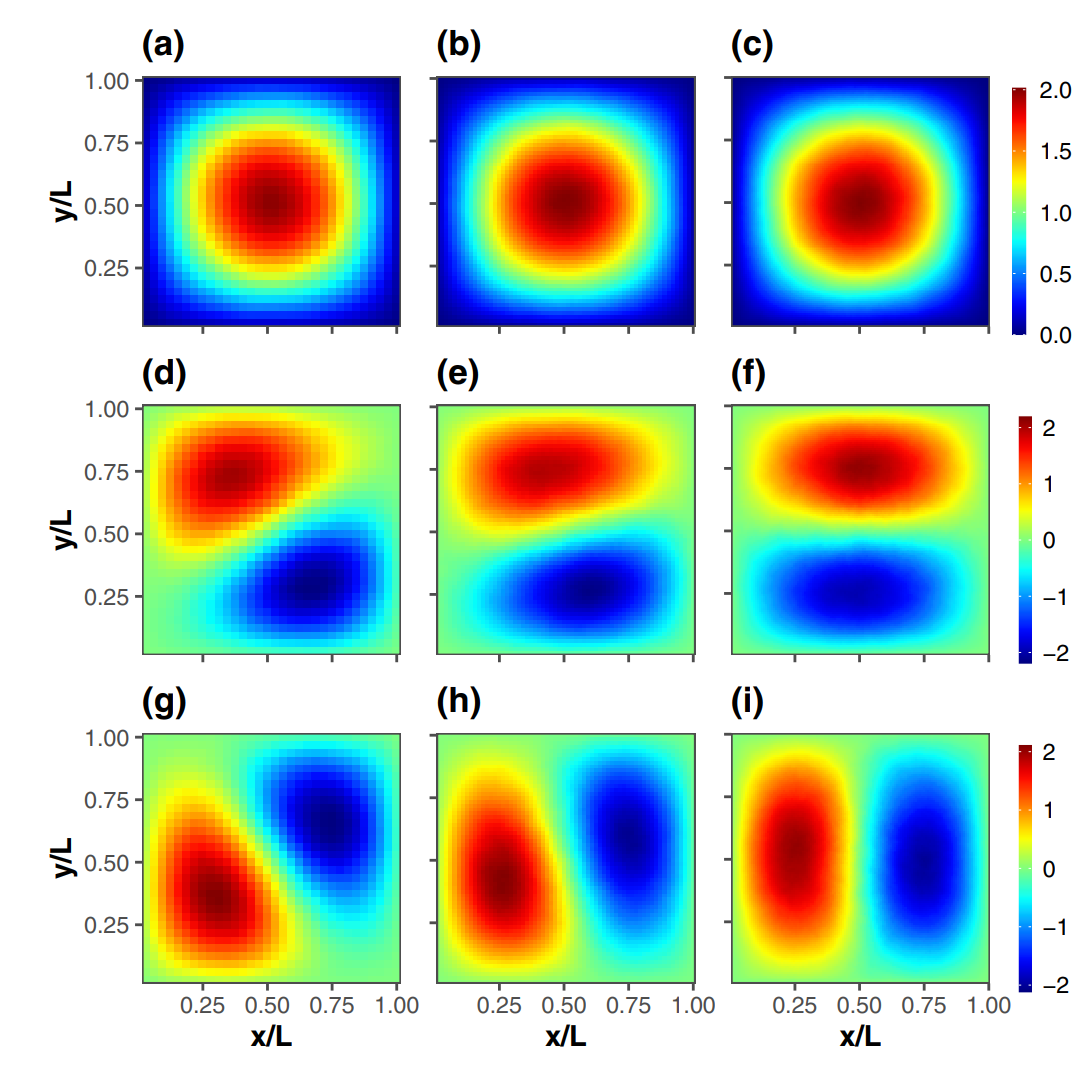
图2. btw模型临界态的本征微观态标度空间分布。第一大本征微观态展示在（a）-(c),分别对应尺度l=32,64和128， 第二大本征微观态展示在（d）-(f)，第三大本征微观态展示在(g)-(i)。

此外，通过对第一大本征微观态的相关物理量进行有限尺度标度分析，可以确定沙堆模型的临界指数（见图3）。由此得到的临界指数，即使模拟系统的尺度不大，也能获得比较精确的值，这是因为第一本征微观态涉及整体关联的有限尺度效应，其相关物理量具有渐近的有限尺度标度性。

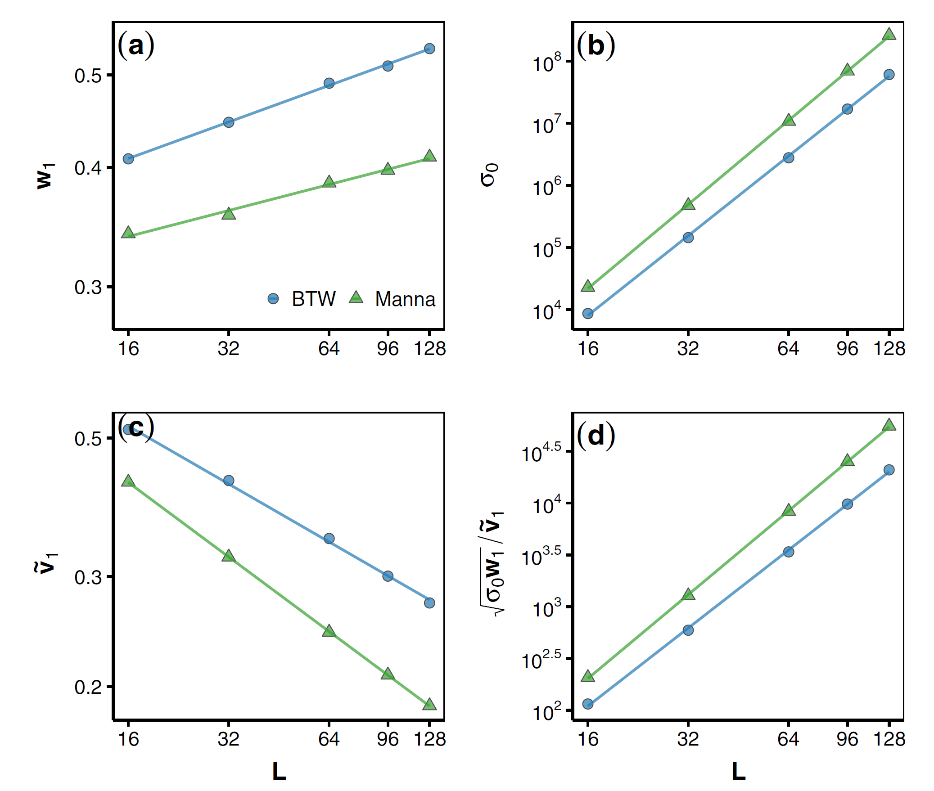
图3. 第一大本征微观态相关物理量的有限尺度标度分析与临界指数

上述研究结果以“eigen microstates in self-organized criticality”为题于2024年4月11日正式发表在物理学国际权威杂志physical review e。昆明理工大学理学院系统科学系张永文副教授为论文的第一作者和通讯作者，北京师范大学陈晓松教授为共同通讯作者，刘卯鑫副教授、胡高科博士和刘腾博士为合作者。该研究得到了国家自然科学基金青年项目（项目编号：12305044）、国家自然科学基金重点项目（项目编号：12135003）、国家重点研发计划（项目编号：2023yfe0109000）和中国博士后基金（项目编号：2023m730299）的资助。

文章链接：

doi: 10.1103/physreve.109.044130

供稿：刘卯鑫

编辑：郝林青

审核：李   辉