北京师范大学系统科学学院-yb亚博全站首页

量子相变是一类与量子效应相关的相变与临界现象。深入研究量子相变对于理解复杂量子多体系统的丰富涌现现象具有重要意义。传统的量子相变理论以朗道相变理论为基本框架，需要预先确定描述相的序参量。然而，一般复杂量子多体系统的序参量难于确定，给当前量子多体研究带来一系列重大挑战。

相变序参量难以确定的困难不仅存在于量子相变的研究中，而且同样是复杂系统相变与临界现象研究中长久以来面临的挑战。为应对这一挑战，北京师范大学系统科学学院陈晓松教授团队提出了统计系综的本征微观态方法，该方法基于统计物理的基础——系综理论。与吉布斯系综理论讨论哈密顿系统的微观态概率分布函数不同，本征微观态理论采用本征微观态及其时间演化和本征值描述复杂系统。本征微观态的概率分布由本征值平方表示，本征微观态取代原始微观态刻画复杂系统，起到了复杂系统微观到宏观的桥梁作用，展现了复杂系统的集体行为。本征微观态理论指出：本征微观态凝聚对应相的涌现及相变，对应本征值为相变序参量。这一新的相变理论——本征微观态凝聚理论——可视为玻色-爱因斯坦凝聚理论的推广。目前，本征微观态方法已成功应用于不同维数的伊辛模型的平衡态相变、群体运动vicsek模型的非平衡相变 ，以及地球表面温度、大气臭氧分布和演化、中国股市价格波动等复杂系统。最近，该团队建立了本征微观态的重整化群理论，一方面将系综的本征微观态思想和临界现象的深刻关系提升到了更高的理论高度，同时也从实用角度给出了一整套能描述包括非哈密顿系统在内的一般复杂系统相变与临界现象研究的理论框架 。

现在，陈晓松教授带领团队进一步将本征微观态方法推广到量子系统。对于量子系统，类比于经典系统中的关联矩阵，作者们定义了量子关联矩阵，并由其本征矢量定义了量子系统的本征微观态。量子相变因此可以诠释为本征微观态的凝聚，对应本征值扮演相变序参量的角色。进一步，以量子拉比模型为例具体实施了量子版本的本征微观态凝聚方案。作者团队长期关注的量子拉比模型是量子光学、量子信息、凝聚态物理领域的基本模型，由于所谓超强耦合的实验实现以及包括作者团队在内的研究组关于超辐射相变的突破性研究，特别是近来超辐射相变的实验实现，使得量子拉比模型也俨然成为了研究量子相变与临界现象的良好平台。通过解析计算和数值计算，本征微观态方法可以得到量子拉比模型超辐射相变的临界点、临界指数和标度函数。可以预期，本征微观态方法将进一步应用于更复杂的量子相变问题，特别是那些难以确定序参量的相变问题。相关成果以“quantum phase transition and eigen microstate condensation in the quantum rabi model”为题发表在physica a: statistical mechanics and its applications, 630, 129210,(2023)。该工作获得了国家自然科学基金委重点项目“复杂系统相变临界现象”的支持。

文章信息：gaoke hu, maoxin liu, xiaosong chen.quantum phase transition and eigen microstate condensation in the quantum rabi model.physica a: statistical mechanics and its applications, 630, 129210,(2023)。

文章链接：https://doi.org/10.1016/j.physa.2023.129210

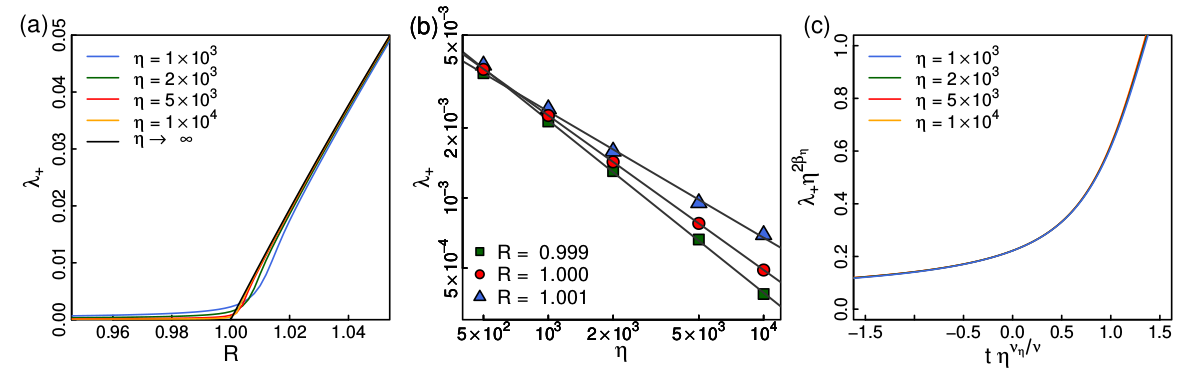
图1. (a) 在不同频率比η，本征值作为耦合强度r的函数。(b) 作为频率比函数的双对数表示。在临界点rc="1.000，得到斜率为    的直线，偏离临界点变为曲线。(c)   在临界点附近的有限   标度函数。  

   供稿：刘牟鑫  

   审核：王大辉  

   编辑：郝林青