gemma de las cuevas* and toby s. cubitt

论文摘要

spin models are used in many studies of complex systems because they exhibit rich macroscopic behavior despite their microscopic simplicity. here, we prove that all the physics of every classical spin model is reproduced in the low-energy sector of certain “universal models,” with at most polynomial overhead. this holds for classical models with discrete or continuous degrees of freedom.we prove necessary and sufficient conditions for a spin model to be universal and show that one of the simplest and most widely studied spin models, the two-dimensional ising model with fields, is universal. our results may facilitate physical simulations of hamiltonians with complex interactions.

论文全文请参见：

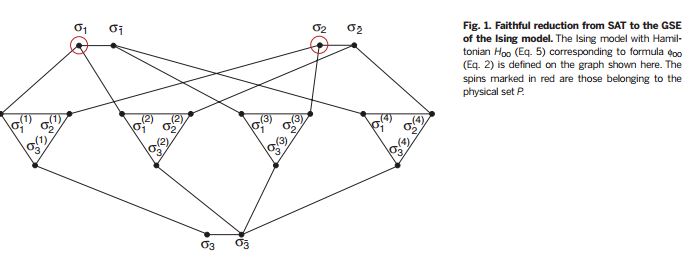
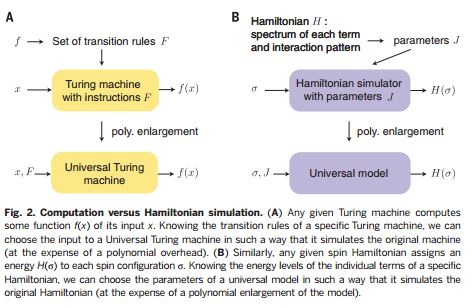
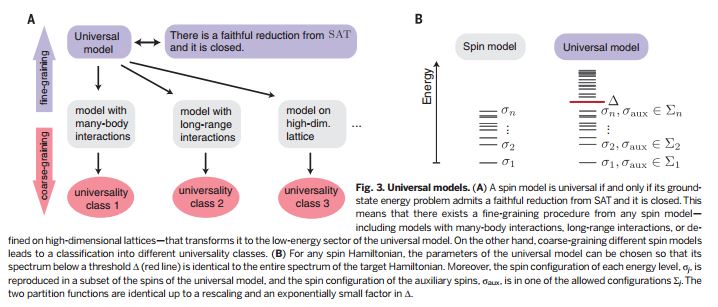
science杂志为此文配发了短评：

one model to rule them all?

the idea of finding an all-encompassing model to describe the world around us has appealed to generations of scientists. although we are very far from this ultimate goal, more modest steps can be taken if we focus on particular problems. de las cuevas and cubitt used concepts borrowed from computer science to show that all classical spin models (introduced initially to study magnetism) can be solved by tackling a slightly more complex, universal model (see the perspective by wehner). thanks to these findings, it may be possible to physically simulate systems with complex interactions, using the well-understood two-dimensional ising model with fields.

science, this issue p. ; see also p. 

北京师范大学系统科学学院-yb亚博全站首页

stephanie wehner

grappling with our desire to understand nature, we construct models of the specific systems that we wish to study. unsurprisingly, such models are generally highly tailored to the system of interest. but are all these models really that distinct? or, could there be a universal model that can somehow describe the behavior of any system we could think of? on page  of this issue, de las cuevas and cubitt () venture out to weave ideas from physics and computer science in an attempt to answer this question for all classical spin models.

评述请参见：